Double Markovian relations
This page provides the lists of graph pairs from Remark 3.33 in our paper The geometry of Gaussian double Markovian distributions.
In the table below, the “tasks” for ground set sizes 3, 4 and 5 are provided in separate files. There may be comment lines prefixed with a # symbol. Each record consists of three lines: R = followed by the CI structure in the canonical variable ordering, G = followed by the list of edges of the first graph and H = followed by the list of edges of the second graph. Records are separated by an empty line.
NOTE: The challenge as stated in v1 of the arXiv paper is wrong (a fault in symmetry reduction). Instead of 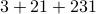 we have
we have 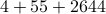 models of connected graphs up to symmetry.
models of connected graphs up to symmetry.
# Have 8 connected graph pairs to consider # There are 4 models up to twisted symmetry R = 001111 G = 1-3, 2-3 H = 1-3, 2-3 R = 011011 G = 1-3, 2-3 H = 1-2, 2-3 ...
This data is computed as follows: first all connected graphs on the given number of vertices are enumerated and representatives modulo the symmetric group (isomorphic graphs yield isomorphic CI structures) are computed. For all pairs of graphs 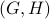 where
where  is reduced modulo symmetry and
is reduced modulo symmetry and 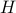 is arbitrary connected, the CI structures are computed and reduced modulo the twisted symmetric group (permutation isomorphy and duality). For each resulting orbit of CI structures, one graph pair is recorded in the file. Deciding smoothness for this graph pair settles the whole orbit.
is arbitrary connected, the CI structures are computed and reduced modulo the twisted symmetric group (permutation isomorphy and duality). For each resulting orbit of CI structures, one graph pair is recorded in the file. Deciding smoothness for this graph pair settles the whole orbit.
| Relations | ||
| tasks-3.log | 4 | |
| tasks-4.log | 55 | |
| tasks-5.log | 2644 |
Partial results on geometric models
The above lists contain different CI structures which may still have the same (geometric) model because double Markovian relations are not complete.
A relation is complete if it is an intersection of realizable gaussoids. The completion of a CI structure is the superset which contains all CI statements which vanish on the model. This puts complete relations and models into a bijective correspondence. Unlike for ordinary undirected graphical models, there is no known combinatorial procedure to list the complete relation for its model. The completion can be computed by multiple invocation of the Positivstellensatz on the semialgebraic set defining the model, but this is very costly.
Instead, we use here orientable gaussoids. Orientable gaussoids are an approximation to realizable gaussoids (every realizable one is orientable, the converse is generally not true, but it holds for  and
and 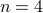 ). Thus, the completion of a CI structure can be approximated by intersecting all orientable gaussoids containing the structure. The obtained “o-completion” is necessarily a subset of the true completion and if two CI structures have the same o-completion, then they have the same completion. Since the o-completion is computable quickly using multiple SAT solver invocations on the gaussoid orientability axioms, this gives a practical way of approximating the model and finding CI structures which are not related by symmetry but still must have the same model.
). Thus, the completion of a CI structure can be approximated by intersecting all orientable gaussoids containing the structure. The obtained “o-completion” is necessarily a subset of the true completion and if two CI structures have the same o-completion, then they have the same completion. Since the o-completion is computable quickly using multiple SAT solver invocations on the gaussoid orientability axioms, this gives a practical way of approximating the model and finding CI structures which are not related by symmetry but still must have the same model.
The following table groups the relations from the previous table by o-completions. As mentioned above, this is a coarsening of the division by geometric models:
| Relations | ||
| o-completions-3.log | 4 | |
| o-completions-4.log | 29 | |
| o-completions-5.log | 472 |
These numbers are upper bounds on the numbers of geometric double Markovian models on the given number of random variables. For 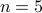 we do not know how precise they are. In addition to the format of the previous files, the o-completions-*.log list one graph pair representative for each orbit modulo symmetry for each o-completion. It also indicates whether the o-completion or its dual is a Markov network. In this case, it is clear that the o-completion coincides with the completion.
we do not know how precise they are. In addition to the format of the previous files, the o-completions-*.log list one graph pair representative for each orbit modulo symmetry for each o-completion. It also indicates whether the o-completion or its dual is a Markov network. In this case, it is clear that the o-completion coincides with the completion.