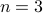Uniform gaussoids

Uniform gaussoids are orientations of the empty gaussoid. Since the supporting gaussoid is empty, all symbols 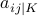$a_{ijtK}$ get signs in 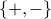{+, -} . The variables use the canonical ordering vars3.txt, vars4.txt.

Downloads

We enumerated uniform gaussoids for 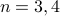n=3,4 :

Realizability of uniform 4-gaussoids

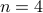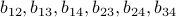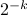To search realizing matrices for gaussoids, it suffices to look for positive-definite matrices with all 1s on the diagonal. For the n=4 case this leaves 6 unknowns $b_{12}, b_{13}, b_{14}, b_{23}, b_{24}, b_{34}$ in the upper triangle of the matrix. We first generated random positive-definite matrices with off-diagonal entries $2^{-k}$ . Of the 46 symmetry classes of uniform 4-gaussoids, 30 were found to be realizable by these matrices. For one of the remaining 16 classes, a bi-quadratic final polynomial was found, and the remaining 15 classes were realized using SCIP.

Our SCIP input files are available as an archive: u4-scip.tar.bz2. The numbering of the files follows Table 2 in the paper. We proceed to explain the contents of the pip files. The 6 unknowns can be supposed to be positive and, given a uniform gaussoid, are endowed with the appropriate signs inside the unknown realizing matrix. The signs of the 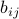$b_{ij}$ are defined by the gaussoid since 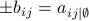$pm b_{ij} = a_{ijtemptyset}$ . Polynomial inequalities arising from the principal and almost-principal minors of that matrix describe the gaussoid's realization space. Since the gaussoid is uniform, there are no equalities, and we flip signs such that all polynomials are to be positive.

The contents of Table 2 are also available as a text file: table2.txt. There is a sage program to verify it: check-table2.sage.

Enumeration details

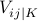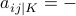We can use one Boolean variable $V_{ijtK}$ to represent the sign of each variable. The convention $a_{ijtK} = -$ if and only if 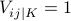$V_{ijtK} = 1$ turns multiplication of signs into addition in the field 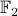$mathbb{F}_2$ . To describe uniform gaussoids, we specialize the explicit listing of compatible assignments for oriented gaussoids to the uniform case. After simplification this gives the formula:

(a^b)->(b^c^d)

These are the files ucnf* in the table below.

Orientations of a given gaussoid

More generally, we have a procedure to print a cnf describing all orientations of a given gaussoid. It works by mutilating all edge trinomials according to the gaussoid and adding specific compatibility clauses depending on how the mutilated polynomial turns out.

Since all symbols which remain after mutilation are in 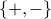{+, -} , we use the same binary variable encoding as described for uniform gaussoids.

	c2d	time	cachet	time	sharpSAT	time	bdd_minisat_all	time
ucnf3	20	0.00	*	0.01	*	0.00	ucnf3-list.txt	0.00
ucnf4	5376	0.04	*	0.04	*	0.02	ucnf4-list.txt	0.02
ucnf5	878349984	1383	*	1212	*	15071	-	-
o1…13	*	0.00	*	0.01	*	0.00	-	-
o1…14	*	0.04	*	0.04	*	0.02	-	-
o1…15	*	1739	*	1454	*	12796	-	-

It suffices to replace 0 with + and 1 with - in the output of minisat2binary.pl to obtain a human-readable listing of uniform gaussoids:

$ minisat2binary.pl <ucnf3-list | tr '01' '+-' >ucnf3-list.txt