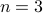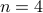Oriented gaussoids
Download
We enumerated all oriented gaussoids for 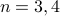 :
:
Enumeration details
By definition an oriented gaussoid is an assignment of symbols 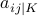 to signs
to signs 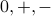 which is compatible with all edge trinomials. Let
which is compatible with all edge trinomials. Let 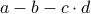 be an edge trinomial with
be an edge trinomial with 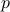 -variables removed. Compatibility with this trinomial
can be expressed with the formula
-variables removed. Compatibility with this trinomial
can be expressed with the formula
((a=0&b=0)->(c=0|d=0))& (((a=0&b=+)|(a=-&b=0)|(a=-&b=+))->((c=+&d=-)|(c=-&d=+)))& (((a=0&b=-)|(a=+&b=0)|(a=+&b=-))->((c=+&d=+)|(c=-&d=-)))
which is a compressed listing of all compatible assignments as a case distinction
on the values of  and
and 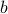 . Another formula for compatibility is
. Another formula for compatibility is
(a=+|b=-|(c=+&d=-)|(c=-&d=+))<->(a=-|b=+|(c=+&d=+)|(c=-&d=-))
which reads: there is a positive term if and only if there is a negative term. The latter formula is shorter and more symmetric but the former was solved faster most of the time in our tests.
To encode the three values 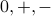 we introduce two variables
we introduce two variables 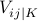 and
and 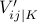 for every symbol
for every symbol 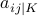 and use the following translation
table:
and use the following translation
table:
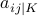 | 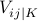 | 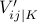 | |
| 0 | 1 | 1 | |
| + | 1 | 0 | |
| - | 0 | 1 |
The fourth assignment of Boolean variables is forbidden explicitly in the
cnf file. Since there are twice as many variables as with gaussoids, we
have to choose another ordering. If the symbol 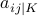 has canonical
index
has canonical
index 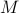 , then
, then 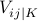 gets index
gets index 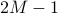 and
and 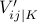 gets
gets 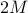 .
.
An alternate encoding uses three variables 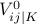 ,
, 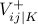 , and
, and
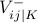 for each symbol and the table:
for each symbol and the table:
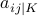 | 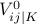 | 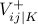 | 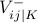 | |
| 0 | 1 | 0 | 0 | |
| + | 0 | 1 | 0 | |
| - | 0 | 0 | 1 |
With this encoding, we can exploit the built-in support for E-clauses of the c2d solver. An E-clause is a clause in a cnf formula which must be satisfied by satisfying exactly one literal. Note that some solvers, in particular cachet, throw a parser error when they encounter an eclauses line in a DIMACS file while others, in particular sharpSAT, ignore it and compute unintended results.
The variables 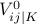 ,
, 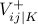 , and
, and 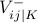 here get
indices
here get
indices 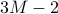 ,
, 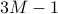 and
and 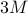 respectively.
respectively.
There are four possibilities to combine formula and variable encoding. The suffix “f” indicates that the second formula was used and the suffix “v” that the second variable encoding was used.
| c2d | time | cachet | time | sharpSAT | time | bdd_minisat_all | time | |||||
| ocnf3 | 51 | 0.04 | * | 0.02 | * | 0.00 | ocnf3-list.txt | 0.00 | ||||
| ocnf4 | 34873 | 2.46 | * | 3.51 | * | 0.68 | ocnf4-list.txt | 1.62 | ||||
| ocnf5 | OOM | - | 54936241913 | 48126 | * | 196298 | - | - | ||||
| ocnf3f | * | 0.16 | * | 0.02 | * | 0.00 | - | - | ||||
| ocnf4f | * | 10.42 | * | 3.12 | * | 1.97 | - | - | ||||
| ocnf5f | OOM | - | * | 129868 | * | 363406 | - | - | ||||
| ocnf3v | * | 0.06 | - | - | - | - | - | - | ||||
| ocnf4v | * | 1.88 | - | - | - | - | - | - | ||||
| ocnf5v | OOM | - | - | - | - | - | - | - | ||||
| ocnf3fv | * | 0.04 | - | - | - | - | - | - | ||||
| ocnf4fv | * | 0.84 | - | - | - | - | - | - | ||||
| ocnf5fv | OOM | - | - | - | - | - | - | - |
The following perl script implements the translation table for the first variable encoding, which was used in ocnf{3,4,5}:
#!/usr/bin/perl -an my %conv = ('11' => '0', '10' => '+', '01' => '-'); chomp; print $conv{$_} for m/../g; print "\n";
We obtain a string composed of 0, + and - which encodes the orientation
of the supporting gaussoid under the canonical numbering of  -variables.
The listings linked in the table were obtained with:
-variables.
The listings linked in the table were obtained with:
$ minisat2binary.pl <ocnf3-list | binary2oriented.pl >ocnf3-list.txt